Astronomy Object of the Month: 2021, February
< previous Archive next >
Freely falling bodies in standing-wave spacetime
The phenomena of standing waves
is well known in mechanical and electromagnetic setting where the wave has the maximum and minimum amplitude at
the antinodes and nodes, respectively. In context of exact solution to
Einstein
Field equations, we analyze a spacetime which represents standing gravitational waves in an expanding Universe.
General Relativity is the theory describing
gravity in terms of the geometry of spacetime. The three spatial dimensions and one time dimension which make up this
spacetime become a dynamic entity. Earlier the fundamental interactions used to be studied where the spacetime was a
background stage and particles and field were the main characters. Now in the study of gravity the spacetime itself becomes an active participant.
When you give a quick, sudden movement to a string tied to a wall or when you pluck a string on a guitar, standing waves
are produced. In context of Gravity, there exist these ripples of spacetime known as
Gravitational waves. One can then raise a
question whether standing gravitational waves exist. More precisely: do Einstein Field equations admit solution which can
be interpreted as standing gravitational wave? One can
superimpose two electromagnetic waves since its underlying theory, electromagnetism is linear but a superposition of
gravitational waves is complicated owing to the non-linear nature of gravity.
It turns out under certain conditions a spacetime, known as
Gowdy spacetime, can be studied which represents a non-linear superposition of gravitational waves. We study a
toy model which represents an expanding Universe filled
with gravitational waves which are interacting and forming standing
gravitational waves. The geometry of this 4-dimensional spacetime has spatial sections having a torus topology.
This represents a
3-torus which is like a higher dimensional donut. Instead of joining the opposite sides of a square tile to form a 2-torus,
you join the opposite sides of a cube in order to get a 3-torus. Figure 1 illustrates how standing waves can be studied in a 2-torus
configuration. The basic idea we pursue is to have a family of observers immersed in a spacetime whose spatial geometry is of a
3-torus and try to understand how freely-falling test masses would behave.
When one is reading this article on a screen there exists three directions, one ‘longitudinal’ and two ‘transverse’.
Longitudinal is the direction towards or away from the screen (say Z-axis) and transverse is a direction parallel to the
screen (one in X-axis and one in Y-axis). Generally when a gravitational wave is perpendicularly incident on a ring of particles
they are deformed into an ellipse and return back to the original shape in the transverse direction. We analyze such a behavior
in our spacetime. We also see what will happen to a set of particles in the direction of the wave, i.e, in the longitudinal direction.
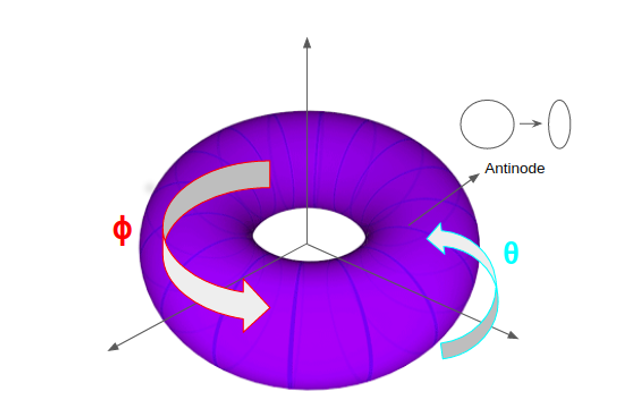
The standing gravitational waves in our spacetime are in Z direction. We found that in the direction of the wave the particles are attracted to the antinodes of the wave. One can imagine that as the amplitude of the wave is maximum at the antinodes it would imply a concentration of gravitational energy. This would mean a source of gravitational potential hence it should act as a region of attraction for particles. This is what we found in our spacetime that particles are on average attracted to the antinodes. At these antinodes, we had freely-falling observers who try to analyze the behaviour of gravitational waves in the transverse direction. And what we found that a ring of test masses is permanently deformed in the transverse direction. This permanent effect left behind after a gravitational wave has passed is known as gravitational wave memory.
The gravitational waves which are detected on Earth are of astrophysical origins. They are generated by the compact objects (like Black Holes, Neutrons Stars) very far away from Earth. The nature of gravitational waves which is detected is of transverse nature. In principle there exists longitudinal and ‘Coulombic’ effect which are overshadowed since the compact objects are very far away. If a gravitational wave is in Z direction, then:
i) The transverse effect is to compress a ring of particles in XY direction to an ellipse.
ii) The longitudinal effect is to compress a ring of particles in Z direction to an ellipse.
iii) The Coulomb effect is to squash a sphere of particles in Z direction to an ellipsoid.
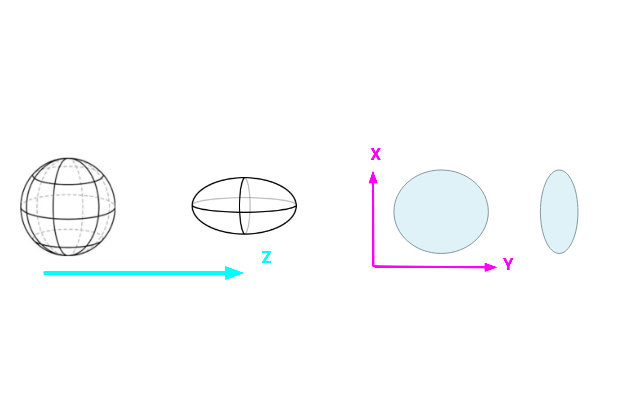
The spacetime we study has just gravitational waves all around. Therefore one can look for these additional effects of gravitational waves in our spacetime. In our work we found a Coulomb effect of the standing gravitational wave and a sphere of test masses in our spacetime will get squished into an ellipsoid in the direction of the wave. This is illustrated in Figure 2.
Although the spacetime we study is a toy model nevertheless this attraction of particles at the antinodes and the longitudinal effect indicate towards the non-linear effects one might expect when superimposing two gravitational waves. A future investigation would be how an electromagnetic wave couples to gravity and what would be the nature of particles in that spacetime.
Original publication: Freely-falling bodies in standing-wave spacetime; Sebastian J. Szybka, Syed U. Naqvi, Phys. Rev. D, 103, 024011 (2021).
Presented results are a part of research conducted at the Department of Relativistic Astrophysics and Cosmology of the Jagiellonian University’s Astronomical Observatory.
|
Syed Naqvi Astronomical Observatory Jagiellonian University S.Naqvi [at] oa.uj.edu.pl |


