Astronomiczny Obiekt Miesiąca: Maj 2019
< poprzedni Archiwum następny >
Nowa metoda konstruowania niejednorodnych modeli kosmologicznych
Badania niejednorodnych modeli kosmologicznych są aktywnie rozwijaną gałęzią ogólnej teorii względności i kosmologii. Opracowując nowe techniki
rozwiązywania fizycznie motywowanych zagadnień
teorii grawitacji Einsteina poszerzamy naszą wiedzę o Wszechświecie o nieznane zjawiska i wyznaczamy przyszłe kierunki badań.
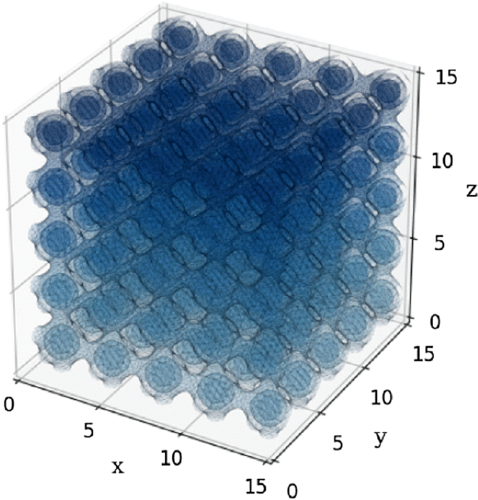
Ilustracja 1: Izolinie gęstości materii w rozważanym modelu tworzące nieskończoną, periodyczną sieć zagęszczeń i rozrzedzeń. Źródło: Publikacja zespołu.
Współczesna kosmologia opiera się na standardowym modelu kosmologicznym, w którym jednorodna i izotropowa przestrzeń wypełniona jest materią opisywaną przez płyn doskonały. Mimo swej prostoty model ten nadaje się do opisu globalnej ewolucji Wszechświata oraz do analizy prowadzonych w nim obserwacji astronomicznych. Główną jego wadą jest jednak brak struktur kosmologicznych, gromad galaktyk, filamentów i pustek, z czym wiąże się niepewność co do interpretacji wyników obserwacyjnych.
Niejednorodne modele kosmologiczne tworzą klasę rozwiązań równań teorii względności, które zawierają i tworzone są przez niejednorodności materii i geometrii o potencjalnie dowolnie dużym kontraście. Pozwalają one śledzić ewolucję struktur, a także badać efekty powodowane lepkością materii, które były istotne we wczesnym Wszechświecie. Podstawową ich zaletą jest możliwość analizy wpływu struktur na propagację światła, co jest niezmiernie ważne dla poprawnej interpretacji obserwacji prowadzonych obecnie. Ponadto modele niejednorodne wykorzystuje się w badaniach problemu uśredniania w kosmologii, w którym pytamy o to, czy i w jaki sposób można opisywać dynamikę niejednorodnej czasoprzestrzeni poprzez efektywną jednorodną czasoprzestrzeń.
Ścisłych niejednorodnych rozwiązań równań Einsteina znaleziono do tej pory jednak bardzo niewiele, a te nieliczne znane posiadają zwykle niepożądane symetrie. Dlatego też tak ważne jest poszukiwanie nowych modeli niejednorodnych o fizycznie interesujących własnościach.
W omawianej pracy przedstawiona została konstrukcja modelu kosmologicznego zawierającego periodyczny rozkład pyłowych niejednorodności. Konstrukcja ta ma charakter perturbacyjny, jednakże w odróżnieniu od innych tego typu podejść, dzięki ścisłej kontroli równań perturbacyjnych wyższych rzędów uzyskano model o wysokim kontraście gęstości. Mimo znacznej złożoności problemu przyjęta strategia konstrukcji pozwoliła zachować jego metrykę we względnie prostej formie. Dynamika tego modelu istotnie odróżnia go od modelu jednorodnego, wobec czego nie może on być przybliżany przez ewolucję zaburzeń na ustalonym tle. Przeprowadzona analiza propagacji światła w otrzymanym modelu wykazała, że jego funkcja odległości znacznie odbiega od funkcji odległości modelu uśrednionego i silnie zależy od pozycji obserwatora względem niejednorodności.
Wyniki pracy wskazują, że dla prawidłowej oceny wyników obserwacji astronomicznych o charakterze kosmologicznym niezbędne jest uwzględnienie obecności struktur we Wszechświecie. Przede wszystkim dotyczy to struktur lokalnych, bliskich dla obserwatora. Zaprezentowany w pracy schemat konstrukcyjny okazał się być możliwy do przeprowadzenia, a uzyskany model mógł być poddany skutecznej analizie. Ogólny charakter nowo prezentowanego podejścia pozwoli w przyszłości na dalsze jego rozszerzenia i umożliwi badania jeszcze bardziej realistycznych modeli kosmologicznych.
Oryginalna publikacja: Perturbatively constructed cosmological model with periodically distributed dust inhomogeneities; Szymon Sikora, Krzysztof Głód, Physical Review D, 99, 083521 (2019).
Przedstawione wyniki są częścią badań prowadzonych w Zakładzie Astrofizyki Relatywistycznej i Kosmologii Obserwatorium Astronomicznego UJ. Praca została wsparta przez grant "Conceptual Problems in Unification Theories" Fundacji Johna Templetona.
|
Krzysztof Głód Obserwatorium Astronomiczne UJ K.Glod [at] uj.edu.pl |


