Analytic models describe extreme geometries, matter supplies and optical depths
Non-linear, coupled partial differential equations of radiative viscous hydrodynamics (or magnetohydrodynamics)
that describe physics of accretion discs are too complex to be exactly
solved analytically in the general case. Usually, analytic models assume
that the accretion is stationary and axially symmetric. For such discs,
useful approximate solutions exist in extreme cases corresponding to
the following three fundamental divisions (as shown in Figure 1):
- Geometry: vertically "thin" versus "thick" discs
- Mass supply rate: "sub" versus "super" Eddington accretion rate
- Optical depth: "opaque" versus "transparent" discs
Subsection 3.1. Thin discs covers accretion disc models with H/R < 1 that includes Shakura-Sunyaev, slim and adafs.
Subsection 3.2. Thick discs covers accretion disc models with H/R > 1 that includes Polish doughnuts and ion tori.
|
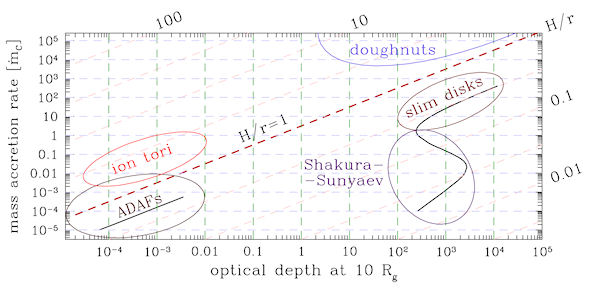
The main types of analytic accretion disc
models in the parameter space of different geometries (i.e. vertical
thickness), matter supplies (i.e. accretion rates) and optical depths.
Credit: Aleksander Sadowski (2009)
|
Extreme geometries: vertically "thin" and "thick" accretion discs
A thin discs has its "vertical" (i.e. across the
disk plane) extension much smaller than its "radial" (along the plane)
extension, 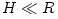 . This means that the disc structure depends mostly on the radial coordinate 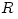 and may be described by ordinary differential equations. Thick discs have toroidal shapes with 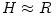 . In this case, the analytic solution is possible because simplifying assumptions concerning mostly physics. Detailed models of thin and thick discs are described in the sub-sections of this Scholarpedia article: 3.1. Thin discs, 3.2. Thick discs.Extreme mass supply : "sub" and "super" Eddington accretion rates
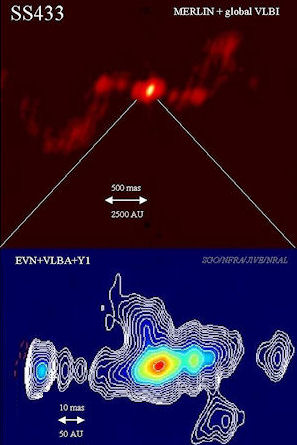
Radio maps of SS433, a source containing a super-Eddington accretion disc. SS433 may be a Galactic prototype of the ultraluminous X-ray sources ( ULXs) found in other galaxies.
|
|
The accretion rate is defined as the instantaneous mass flux through a spherical surface 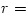 const
inside the disc. In non-stationary accretion discs accretion rate
depends on both time and location, but in stationary disc models with no
substantial outflows (no strong winds) it is const
inside the disc. In non-stationary accretion discs accretion rate
depends on both time and location, but in stationary disc models with no
substantial outflows (no strong winds) it is
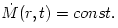
Accretion discs may be divided into two classes, depending on whether
accretion rate is much smaller than, or comparable to the
characteristic Eddington accretion rate, that depends only on the mass
of the central accreting object 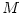 , ,
![{\dot M}_{Edd} = {L_{Edd}/c^2} =1.5 \times 10^{17}\,({M /M_0})\,[{\rm g}/{\rm sec}].](12-analytic-models_files/8321781df35fef242e092b1e92008de0.png)
Here 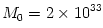 [g] denotes the mass of the Sun, and [g] denotes the mass of the Sun, and  is the Eddington luminosity (radiation power), familiar from the theory
of stellar equilibria: at the surface of a star shining at the
Eddington rate, the radiation pressure force balances the gravity force.
is the Eddington luminosity (radiation power), familiar from the theory
of stellar equilibria: at the surface of a star shining at the
Eddington rate, the radiation pressure force balances the gravity force.
Figure on the left shows radio maps of SS433, a well-known Galactic object with a super-Eddington accretion disc.
A rather common belief that a black hole
cannot accrete at a rate higher than the Eddington one is wrong. In
particular, the Eddington rate is not a limit for the mass growth rate
of a black hole due to accretion, 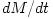 . It could be that . It could be that 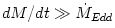 . This is relevant for modeling the cosmological evolution of black holes. . This is relevant for modeling the cosmological evolution of black holes.
|
Extreme optical depth: "opaque" and "transparent" accretion discs
Note: a more detailed discussion of the subject presented in this Section is given in Narayan & Yi,1995, ApJ, 452,710. Optical depth in vertical direction 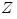 is approximated by is approximated by 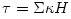 . Here . Here 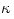 is the opacity coefficient, and is the opacity coefficient, and 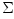 is the surface density, i.e. vertically integrated density. is the surface density, i.e. vertically integrated density.
Opaque discs (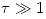 ): Such discs are not very hot, the temperature is much less than the virial temperature, ): Such discs are not very hot, the temperature is much less than the virial temperature, 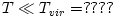 . Simple (and often used) analytic models approximate the flux emitted locally (at a fixed radius . Simple (and often used) analytic models approximate the flux emitted locally (at a fixed radius 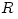 ) from the disk surface by the "diffusive" black body formula, ) from the disk surface by the "diffusive" black body formula, 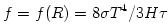 . In calculating spectra, the total flux from whole surface of accretion disc is (roughly) approximated by the Planck formula, . In calculating spectra, the total flux from whole surface of accretion disc is (roughly) approximated by the Planck formula,
![F_{\nu}=4\pi \frac{\nu^3 \cos i}{c^2 d^2}\int^{R_{out}}_{R_{in}}\frac{R}{\exp[h\nu/kT(R)]-1}dR,](12-analytic-models_files/787039c47412cfd9f1b5d3ede5e461c3.png)
where 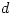 and and 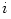 are the distance and inclination angle to the rotation axis,
respectively, as seen by an observer. More advanced models solve
(approximately) radiative transfer equation in the vertical direction (see e.g. REFERENCES SHOULD BE ADDED), considering dependence on the radiation frequency
are the distance and inclination angle to the rotation axis,
respectively, as seen by an observer. More advanced models solve
(approximately) radiative transfer equation in the vertical direction (see e.g. REFERENCES SHOULD BE ADDED), considering dependence on the radiation frequency 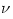 . .
Transparent discs (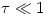 ):
Such discs have relatively high-temperatures and low-densities.
Bremsstrahlung, synchrorton and Copmton radiative processes are most
relevant, ):
Such discs have relatively high-temperatures and low-densities.
Bremsstrahlung, synchrorton and Copmton radiative processes are most
relevant, 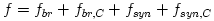 .
They cool down the electrons in the gas much more efficiently than the
ions, and therefore a temperature separation between electrons .
They cool down the electrons in the gas much more efficiently than the
ions, and therefore a temperature separation between electrons 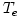 and ions and ions 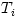 is expected. Radiative cooling by Bremsstrahlung, is expected. Radiative cooling by Bremsstrahlung, 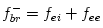 is given by, is given by,
![f_{ei} = n_e n_i c \sigma_T \alpha_f m_e c^2 F_{ei}(\theta_e) \,\, [{\rm erg \,\, cm^{-3} \,\, s^{-1}}],](12-analytic-models_files/d03d9f854b68f4e7f2b920f4b52c1e79.png) where where 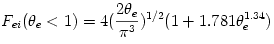 and and ![F_{ei}(\theta_e>1) = \frac{9 \theta_e}{2\pi}[\ln(1.123 \theta_e + 0.48) + 1.5]](12-analytic-models_files/6a2d461488cfbfed46f7204661b87431.png)
![f_{ee} = n_e^2 c r_e^2 \alpha_f m_e c^2 F_{ee}(\theta_e) \,\, [{\rm erg \,\, cm^{-3} \,\, s^{-1}}],](12-analytic-models_files/ed40014b585d85d461411119237f174f.png) where where 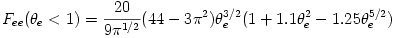 and and ![F_{ee}(\theta_e>1) = 24 \theta_e [\ln(0.5616 \theta_e) + 1.28]](12-analytic-models_files/97176c0ff214a7f6ee73b053a29b81a3.png)
![f_{br,C} = 3\eta_1\{\frac{1}{3}(1-\frac{x_c}{\theta_e})-\frac{1}{\eta_3+1}[(\frac{1}{3})^{\eta_3+1}-(\frac{1}{3\theta_e})^{\eta_3+1}]\} f_{br},](12-analytic-models_files/a667850a40dc8d2ebec7c16c58ef6998.png)
where 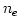 and and 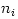 are the number densities of electrons and ions, are the number densities of electrons and ions, 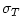 is the Thomson cross-section and is the Thomson cross-section and 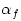 the fine structure constant, the fine structure constant, 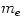 and and 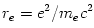 are the electron's mass and radius and are the electron's mass and radius and 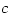 the speed of light. the speed of light. 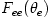 and and 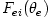 are the radiation rate functions, given by the dimensionless electron temperature are the radiation rate functions, given by the dimensionless electron temperature 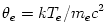 . The Compton enhancement factor . The Compton enhancement factor 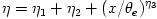 is given by is given by 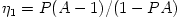 , ,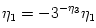 and and 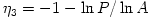 , where , where 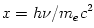 , factor , factor 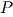 is the probability that a photon scatters and is the probability that a photon scatters and 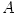 is the mean energy amplification factor by that photon and is the mean energy amplification factor by that photon and 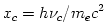 . If a magnetic field . If a magnetic field 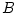 is present, there is also radiative cooling by synchrotron emission: is present, there is also radiative cooling by synchrotron emission:
![f_{syn} = \frac{2\pi}{3c^2}kT_e(R)\frac{d\nu_c^3(R)}{dR}\,, ~~f_{syn,C} = [\eta_1 - \eta_2(\frac{x_c}{\theta_e})^{\eta_3}] f_{syn}\,, ~~ \nu_c = \frac{3 e B}{4 \pi m_e c} \theta_e^2 x_M,](12-analytic-models_files/3f15855f3f86400e7868671eb896a896.png)
where the coefficient 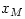 must be numerically calculated from a relativistic Maxwellian distribution of electrons. must be numerically calculated from a relativistic Maxwellian distribution of electrons.
|
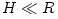 . This means that the disc structure depends mostly on the radial coordinate
. This means that the disc structure depends mostly on the radial coordinate 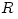 and may be described by ordinary differential equations. Thick discs have toroidal shapes with
and may be described by ordinary differential equations. Thick discs have toroidal shapes with 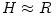 . In this case, the analytic solution is possible because simplifying assumptions concerning mostly physics. Detailed models of thin and thick discs are described in the sub-sections of this Scholarpedia article: 3.1. Thin discs, 3.2. Thick discs.
. In this case, the analytic solution is possible because simplifying assumptions concerning mostly physics. Detailed models of thin and thick discs are described in the sub-sections of this Scholarpedia article: 3.1. Thin discs, 3.2. Thick discs.

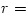 const
inside the disc. In non-stationary accretion discs accretion rate
depends on both time and location, but in stationary disc models with no
substantial outflows (no strong winds) it is
const
inside the disc. In non-stationary accretion discs accretion rate
depends on both time and location, but in stationary disc models with no
substantial outflows (no strong winds) it is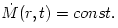
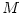 ,
,![{\dot M}_{Edd} = {L_{Edd}/c^2} =1.5 \times 10^{17}\,({M /M_0})\,[{\rm g}/{\rm sec}].](12-analytic-models_files/8321781df35fef242e092b1e92008de0.png)
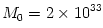 [g] denotes the mass of the Sun, and
[g] denotes the mass of the Sun, and 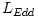 is the Eddington luminosity (radiation power), familiar from the theory
of stellar equilibria: at the surface of a star shining at the
Eddington rate, the radiation pressure force balances the gravity force.
is the Eddington luminosity (radiation power), familiar from the theory
of stellar equilibria: at the surface of a star shining at the
Eddington rate, the radiation pressure force balances the gravity force.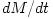 . It could be that
. It could be that 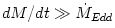 . This is relevant for modeling the cosmological evolution of black holes.
. This is relevant for modeling the cosmological evolution of black holes.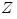 is approximated by
is approximated by 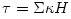 . Here
. Here 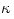 is the opacity coefficient, and
is the opacity coefficient, and 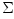 is the surface density, i.e. vertically integrated density.
is the surface density, i.e. vertically integrated density.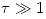 ): Such discs are not very hot, the temperature is much less than the virial temperature,
): Such discs are not very hot, the temperature is much less than the virial temperature, 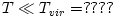 . Simple (and often used) analytic models approximate the flux emitted locally (at a fixed radius
. Simple (and often used) analytic models approximate the flux emitted locally (at a fixed radius 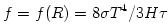 . In calculating spectra, the total flux from whole surface of accretion disc is (roughly) approximated by the Planck formula,
. In calculating spectra, the total flux from whole surface of accretion disc is (roughly) approximated by the Planck formula,![F_{\nu}=4\pi \frac{\nu^3 \cos i}{c^2 d^2}\int^{R_{out}}_{R_{in}}\frac{R}{\exp[h\nu/kT(R)]-1}dR,](12-analytic-models_files/787039c47412cfd9f1b5d3ede5e461c3.png)
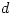 and
and 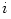 are the distance and inclination angle to the rotation axis,
respectively, as seen by an observer. More advanced models solve
(approximately)
are the distance and inclination angle to the rotation axis,
respectively, as seen by an observer. More advanced models solve
(approximately) 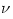 .
.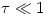 ):
Such discs have relatively high-temperatures and low-densities.
Bremsstrahlung, synchrorton and Copmton radiative processes are most
relevant,
):
Such discs have relatively high-temperatures and low-densities.
Bremsstrahlung, synchrorton and Copmton radiative processes are most
relevant, 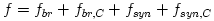 .
They cool down the electrons in the gas much more efficiently than the
ions, and therefore a temperature separation between electrons
.
They cool down the electrons in the gas much more efficiently than the
ions, and therefore a temperature separation between electrons 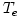 and ions
and ions 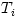 is expected. Radiative cooling by Bremsstrahlung,
is expected. Radiative cooling by Bremsstrahlung, 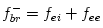 is given by,
is given by,![f_{ei} = n_e n_i c \sigma_T \alpha_f m_e c^2 F_{ei}(\theta_e) \,\, [{\rm erg \,\, cm^{-3} \,\, s^{-1}}],](12-analytic-models_files/d03d9f854b68f4e7f2b920f4b52c1e79.png) where
where 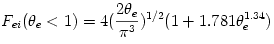 and
and ![F_{ei}(\theta_e>1) = \frac{9 \theta_e}{2\pi}[\ln(1.123 \theta_e + 0.48) + 1.5]](12-analytic-models_files/6a2d461488cfbfed46f7204661b87431.png)
![f_{ee} = n_e^2 c r_e^2 \alpha_f m_e c^2 F_{ee}(\theta_e) \,\, [{\rm erg \,\, cm^{-3} \,\, s^{-1}}],](12-analytic-models_files/ed40014b585d85d461411119237f174f.png) where
where 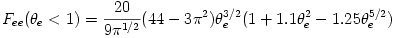 and
and ![F_{ee}(\theta_e>1) = 24 \theta_e [\ln(0.5616 \theta_e) + 1.28]](12-analytic-models_files/97176c0ff214a7f6ee73b053a29b81a3.png)
![f_{br,C} = 3\eta_1\{\frac{1}{3}(1-\frac{x_c}{\theta_e})-\frac{1}{\eta_3+1}[(\frac{1}{3})^{\eta_3+1}-(\frac{1}{3\theta_e})^{\eta_3+1}]\} f_{br},](12-analytic-models_files/a667850a40dc8d2ebec7c16c58ef6998.png)
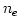 and
and 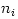 are the number densities of electrons and ions,
are the number densities of electrons and ions, 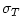 is the Thomson cross-section and
is the Thomson cross-section and 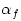 the fine structure constant,
the fine structure constant, 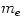 and
and 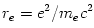 are the electron's mass and radius and
are the electron's mass and radius and 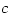 the speed of light.
the speed of light. 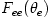 and
and 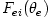 are the radiation rate functions, given by the dimensionless electron temperature
are the radiation rate functions, given by the dimensionless electron temperature 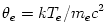 . The Compton enhancement factor
. The Compton enhancement factor 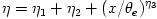 is given by
is given by 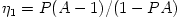 ,
,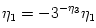 and
and 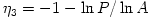 , where
, where 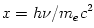 , factor
, factor 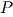 is the probability that a photon scatters and
is the probability that a photon scatters and 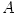 is the mean energy amplification factor by that photon and
is the mean energy amplification factor by that photon and 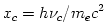 . If a magnetic field
. If a magnetic field 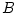 is present, there is also radiative cooling by synchrotron emission:
is present, there is also radiative cooling by synchrotron emission:![f_{syn} = \frac{2\pi}{3c^2}kT_e(R)\frac{d\nu_c^3(R)}{dR}\,, ~~f_{syn,C} = [\eta_1 - \eta_2(\frac{x_c}{\theta_e})^{\eta_3}] f_{syn}\,, ~~ \nu_c = \frac{3 e B}{4 \pi m_e c} \theta_e^2 x_M,](12-analytic-models_files/3f15855f3f86400e7868671eb896a896.png)
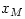 must be numerically calculated from a relativistic Maxwellian distribution of electrons.
must be numerically calculated from a relativistic Maxwellian distribution of electrons.