Pi

Krzysztof Maślanka
(ex Computer-Aided Maniacal Kamikaze)

Motto:

[Salomon] Sporządził też kadź odlewną wyobrażającą morze, okrągłą, długości dziesięciu łokci od krawędzi do krawędzi; [.] obwód zaś jej wynosił trzydzieści łokci.

(1 Krl. 7, 23; por. też 2 Krn. 4, 2-5)

Wstęp

Z przytoczonego powyżej fragmentu I Księgi królewskiej¹ można wywieść jedno z najstarszych znanych oszacowań numerycznych dla sławnej stałej matematycznej - liczby pi. Co prawda, traktowanie biblijnych wersetów jak zbioru zadań z geometrii zakrawa na jawną kpinę, lecz zaręczam, że jest to z pewnością ostatnia rzecz, o którą chciałbym być posądzony. Spróbujmy zatem - choćby w imię naukowej dociekliwości. Nie trzeba specjalnych zdolności rachunkowych, by się przekonać, że rozwiązanie otrzyma się dzieląc obwód wspomnianej kadzi² (30 łokci) przez jej średnicę (10 łokci), a to daje dokładnie³ 3.

Mimo że wartość ta posiada swe tak dobitne uzasadnienie w tekście księgi pisanej przez Autora natchnionego, nie weszła ona, na szczęście, do kanonu dogmatów Kościoła. Uczciwi matematycy staliby się wówczas, automatycznie i bez żadnych wyjątków - heretykami. Wszyscy oni bowiem (oraz niektórzy inni) dobrze wiedzą, że pi to zawsze "trzy z hakiem". Lecz żeby iść w ogień wieczny, i to jeszcze z powodu durnego haka?.

Grubo przed mądrym - choć skądinąd niezbyt cnotliwym - królem Salomonem, ok. roku 2000 p.n.e., byli jeszcze Babilończycy, którzy lansowali wartość 3 1/8  3,125, Egipcjanie (256/81 3,1604; zachował się antyczny dokument z taką właśnie wartością) oraz Chińczycy (także dokładnie 3). Natomiast 250 lat p.n.e. Archimedes, wtedy gdy akurat swym zwyczajem nie moczył się w wannie, wymyślił metodę wpisywanych oraz opisywanych na okręgu wielokątów i używał wynikającej z tego wartości 3 10/71 < pi < 3 1/7, czyli 3,1408 < pi < 3,1428.

Ale to był dopiero początek. Minęło bowiem kilkanaście wieków i na arenie dziejów nauki pojawiło się kilku mądrych ludzi, którzy dowiedli dwóch, skądinąd przykrych, faktów. Najpierw, w roku 1700, Lambert z Legendre'm pokazali, że pi jest niewymierna - nie jest więc ilorazem jakichkolwiek dwu liczb całkowitych, zaś w sekwencji kolejnych cyfr jej rozwinięcia nie ma żadnych, ale to żadnych, prawidłowości. Mówiąc bardziej nowocześnie: całkowita ilość naiwnie rozumianej informacji, która tkwi w tej liczbie jest, ni mniej, ni więcej, tylko - nieskończona.

Po tym fatalnym odkryciu część matematyków (choć, trzeba przyznać, bardzo niewielka) uczepiła się jeszcze złudnej nadziei, jakoby pi mogła być przynajmniej rozwiązaniem jakiegoś równania algebraicznego z całkowitymi współczynnikami. Niestety! W r. 1882 Lindemann rozwiał i tę nadzieję pokazując z kolei, że pi jest tzw. liczbą przestępną. W ten sposób dowiódł też zasadniczej bezsensowności wszelkich prób realizacji marzeń starożytnych Greków - i wielu późniejszych ambitnych maniaków - czyli marzeń o kwadraturze koła.

Jak zatem widać, liczba pi, choć pojęciowo tak prosta, jest w swej najgłębszej istocie nadzwyczaj bogata i skomplikowana. Skoro tak, to nie pozostało nic innego, jak wyliczać w nieskończoność kolejne jej cyfry. Obecnie robi się to zresztą w systemie hexadecymalnym, bo wtedy tych cyfr jest wyraźnie mniej, a poza tym wspomniany na początku "hak" wygląda bardziej tajemniczo: pi = 3,43F6A8885A3.

Do tego mamy dziś jeszcze wszystkie te wspaniałe superkomputery i dzięki nim ponad 6 miliardów 400 milionów dokładnie znanych cyfr dziesiętnego rozwinięcia naszej sławnej stałej. Ale mamy też jeszcze to drażliwe pytanie, na które wypadałoby jakoś odpowiedzieć: a po co komu aż tyle? Przecież żeby obliczyć, na przykład, obwód Drogi Mlecznej, nawet z absurdalną dokładnością lepszą od średnicy protonu, wystarczyłoby raptem 40 cyfr rozwinięcia. Ale 6 miliardów?! Przesada.

Po tym, tak jawnie ciężkim, wstępie zauważmy jeszcze, że - co by nie powiedzieć - stanowi on jednak, w największym skrócie, swoisty wyciąg z dziejów myśli ludzkiej na przestrzeni kilku tysiącleci: od jej zarania aż do czasów najnowszych.

Z drugiej jednak strony, dałbym głowę, że ten i ów z moich Czytelników nabrał dziwnych podejrzeń, że ów wstęp pretendował kiedyś do roli poważnego tekstu, który mi potem odrzucili w jakiejś "Wiedzy i Życiu" czy innej "Delcie", i który w związku z tym przerobiłem naprędce dla "Acta Brutusica". By nie dopuszczać do takich krzywdzących insynuacji przejdziemy teraz wreszcie do spraw lżejszych, na ogół weselszych, ale niekiedy tragicznych.

Rozwinięcie (dziesiętne)

Od czego by tu zacząć? Może tak:

Żyjemy obecnie w bardzo nerwowych czasach. Wystarczy włączyć radio, czy zajrzeć do pierwszej lepszej gazety - a tam same skandale: polityczne, finansowe, gospodarcze, sportowe, towarzyskie, a także ustawiczne eksplozje bomb. Na szczęście wszystko to dzieje się na przemian z epokowymi odkryciami naukowymi. Inaczej można by do reszty oszaleć. Zwłaszcza te liczne dowody sławnych twierdzeń, nad którymi bezskutecznie biedziły się całe pokolenia wielkich matematyków - i to przez tyle lat! A to Wielkie Twierdzenie Fermata; a to Twierdzenie o Czterech Barwach; to znowu zaskakujący dowód Twierdzenia O Zasadniczej Niemożności Zarobienia Więcej Forsy Niż By Się Miało Ochotę Wydać.

Wyznam szczerze, że ja sam, skoro tylko się zbudzę rano, to zaraz pędzę (bez śniadania) do kiosku po "Wyborczą" i nowy numer "The Mathematical Intelligencer", żeby szybko sprawdzić, co tam znowu wybuchło i gdzie tym razem, oraz - czy przypadkiem ktoś nie rozwiązał któregoś z moich ulubionych, a przy tym beznadziejnie trudnych, problemów. Tak było i tego pamiętnego dnia.

Od razu po wyjściu z domu zauważyłem u wszystkich jakieś dziwne, nerwowe podniecenie. Pewien znajomy sąsiad był aż tak zaaferowany, że nawet nie odpowiedział na moje uprzejme powitanie. Inny z kolei lazł przez podwórze jak lunatyk i wtedy zobaczyłem ze zdumieniem, że facet jest w portkach od piżamy! Następny znowuż, krzycząc coś dziko, wskoczył do swego samochodu, ale nie zdążył nawet wyjechać na główną szosę, bo z miejsca wpadł na słup - i to z takim impetem, że urwał zapasowe koło swego pojazdu, a ono potoczyło się w moją stronę, podskakując wesoło na nierównościach bruku. Koło! Coś mi zaczęło świtać w głowie. Czyżby?!. Nie, to niemożliwe.

Przeczuwając coś brzemiennego w skutki i niepojętego zarazem nie byłem w stanie zapytać nikogo, co też się stało. Zresztą - znając siebie - wiedziałem, że i tak nie zdołam wykrztusić nawet jednego słowa. Pędząc jak oszalały do kiosku z gazetami wiedziałem już, że to raczej nie bomba, ani żaden przewrót polityczny, lecz jakieś wielkie odkrycie. Istotnie: nie musiałem nawet zaglądać do "Intelligencera". Wielki nagłówek "Wyborczej" krzyczał na pół pierwszej jej strony: "Nowy, sensacyjny wzór na Pi!", "Szczegóły w niedzielnej Matematycznej Wyborczej".

Wskoczyłem do zatrzymanej taksówki i krzyknąłem kierowcy prosto w ucho: "Gaz do dechy i do Obserwatorium! Zakamycze, Orla 171!". Po drodze, która dłużyła się niemiłosiernie, tłukły mi się po głowie rozmaite sprzeczne myśli: ciekawe, czy już wiedzą?. pewnie dyskutują, próbują odtworzyć dowód. może nawet ktoś to już referuje na zebraniu naukowym!

Gdy jednak dotarłem na miejsce zobaczyłem, że wszystko jest tu tak, jak zawsze. Liczne koty, duże, mniejsze i całkiem małe, obskoczyły mnie z miejsca, nachalnie żądając nakarmienia. Ktoś siedział na drzewie, obżerał się zielonymi jeszcze wiśniami i wypluwał na dół pestki. Inny, gwiżdżąc wesoło, mył wodą z węża samochód, jeszcze inny grzebał w najlepsze w grządkach na pobliskiej działce. Z kuchni dochodziły zapachy przypalonych potraw. Gdzieś w oddali burczała wiertarka i grało radio.

Pospieszyłem do pracowni komputerów. Wybitny uczony X. wpatrywał się z dumą w jakąś kolorową galaktykę na monitorze swego komputera, a senny magister Y. łaził z kąta w kąt i zawzięcie walił plastikową packą w jeszcze bardziej senne muchy. Te przewracały się na plecy, chwilę przebierały w powietrzu łapkami i odlatywały. Pozostali siedzieli przed monitorami nieruchomo, jak zahipnotyzowani.

- Więc wy nic nie wiecie?! - wysapałem zdyszany, nie wierząc własnym oczom.

- Nic - odparł flegmatycznie X. nie przerywając wpatrywania się w monitor. - Spływaj. Tu się pracuje - dodał z niezmąconym spokojem.

Ręce mi opadły. Magister Y. zbliżył się do mnie ze swą packą:

- Wczoraj wypatrzyłem jedną, taką dużą i zieloną - wycedził powoli, bez żadnych wstępów. - Ale mi uciekła. Dzisiaj ją dopadnę. Na pewno - obiecał solennie. Już miał odejść, ale nagle zapytał przyciszonym głosem: - Widziałem przez okno, że przyjechałeś taksówką. Czyżbyś dostał jakiś grant? Przyznaj się lepiej.

Targała mną bezsilna rozpacz. I co tu począć z takimi? Zasiadłem z determinacją do komputera i wdusiłem klawisz. Nie będę z nimi gadał; to nie ma żadnego sensu. Napiszę odezwę i powieszę ją w kuchni - tam, gdzie oni wszyscy przesiadują najczęściej.

Oto tekst owej odezwy in extenso - tak, jak go pamiętam, gdyż nie dysponuję już, niestety, oryginałem:

UCZENI!

Z niekłamaną przykrością, doprawioną do smaku maleńką szczyptą ironii, śmiem Was niniejszym poinformować, że w natłoku:

bardzo ważnych problemów naukowych,
nie cierpiących zwłoki spraw do załatwienia,
nader owocnych wyjazdów za granicę,
licznych bieżących i przyszłych skandali politycznych,
podwyżek cen i obniżek płac,
tryumfalnego pochodu przez świat Windows 95 oraz
fundamentalnej kwestii nieocenionego filtru do wody marki Brita, jako też kuchenki mikrofalowej Daewoo tudzież czajnika bezprzewodowego Philips -

uwadze P. T. Społeczności Naukowej naszego drogiego Obserwatorium kompletnie umknęło rzeczywiście ważne osiągnięcie intelektualne; takie, co to się zdarza raz na 100 (słownie: sto) lat, albo i jeszcze rzadziej. Oto trzej sprytni panowie: David Bailey, Peter Borwein i Simon Plouffe odkryli ostatnio niezwykły "wzór na pi", którego istnienia nie spodziewał się nikt; nikt zatem go wcześniej nie szukał. Wygląda on tak [1]:

Trzeba bezstronnie przyznać, że formuła ta wydaje się podejrzanie prosta; co więcej - nie przypomina ona żadnego innego ze znanych dotąd rozwinięć pi . Ale wbrew pozorom nie jest to jeden z owych przybliżonych wzorków, który z jakichś tam powodów odtwarza kilkanaście cyfr znaczących pi , i jakimi to w dawnych czasach zajmowali się goniący za tanią popularnością matematycy-amatorzy. Jest to rozwinięcie ścisłe, a w dodatku - dość szybko zbieżne.

Każdy naiwny idealista, który kiedykolwiek próbował osobiście policzyć przybliżenie tej czwartej⁴ co do ważności stałej matematycznej, dobrze wie, że dostępne do tej pory w rozmaitych Ryżykach, Gradsteinach, Abramowitzach, Vilenkinach i innych Batemanach szeregi, iloczyny czy ułamki piętrowe (że już nie wspomnę, przez wrodzoną grzeczność, o całkach oznaczonych) zbiegały się do niej nadzwyczaj⁵ wolno. Zacytowana powyżej formuła posiada tę niezwykłą własność, iż kolejny wyraz szeregu daje następną cyfrę znaczącą dziesiętnego rozwinięcia pi , nie zmieniając przy tym cyfr poprzednich! W ten sposób każdy, kto zna elementy choćby (przepraszam za wyrażenie) BASIC-a - czyli każdy z wyjątkiem małpoludów, kotów, humanistów i polityków - może ten wzór wprowadzić, zapuścić, przybliżyć i - uwierzyć⁶.

Dwie rzeczy trzeba tu jeszcze koniecznie dodać: po pierwsze - dowód wzoru (1) jest śmiesznie prosty i mieści się w dwóch linijkach. Ale po drugie - ten prosty dowód został w istocie dorobiony post factum, bowiem wzór (1) znaleziono komputerowo za pomocą rewelacyjnej metody systematycznego szukania twierdzeń matematycznych, zwanej w skrócie PSLQ [2].

Oczywiście, nie jest to najszybciej zbieżna ze znanych formuł na pi; bracia David i Gregory Chudnovsky z Columbia University podali niewiarygodnie⁷ szybko zbieżny związek, z którego np. korzysta sławny i wściekle⁸ drogi pakiet Mathematica fenomenalnego Stevena Wolframa. Jest to wzór w zasadzie tajny, więc ujawnianie go w tym miejscu, to akt sporej odwagi, który, drodzy Uczeni, zechcecie, mam nadzieję, kiedyś docenić:

Podkreślam: także i tu, pomimo obecności trzech bardzo podejrzanych liczb, nie jest to bynajmniej formuła przybliżona, wynik jakiegoś odgadnięcia, sztukowania czy fitowania. Studenci astronomii naszego Obserwatorium (bo nie sądzę, by innym się chciało zniżać do tego) będą uprzejmi sprawdzić, że już pierwszy wyraz tego szeregu (k = 0) daje 13 cyfr znaczących pi, a dodanie każdego kolejnego wyrazu polepsza dokładność o, mniej więcej, dalszych 14 cyfr. Czyż nie jest to piękne?

Wielki wyścig, nieświadomie zapoczątkowany przez Babilończyków, Egipcjan, Chińczyków oraz natchnionego, choć anonimowego, autora I Księgi królewskiej - wciąż trwa! Na jego czele znajduje się aktualnie osobnik o nazwisku Kanada [3]. Wbrew pozorom jest to Japończyk z Tokio o wariackim imieniu Yasumasa, który za pomocą podobnych formuł doliczył się w sierpniu 1995 dokładnie 4,294,967,286 cyfr, i tak się swym wyczynem rozochocił, że w październiku tego samego roku policzył aż 6,442,450,938 cyfr dziesiętnego rozwinięcia pi.

Jednak ambitny ten facet nie może jeszcze wcale spać spokojnie, i to bynajmniej nie z obawy, że mu się przy kolejnym trzęsieniu ziemi chałupa na łeb zawali. Powód jest zupełnie inny: bracia Chudnovsky, posiadacze poprzedniego rekordu, wciąż depczą mu po piętach!

Natomiast pierwszy lepszy smarkacz, któremu nadziany tatuś obstalował Pentium (Intel Inside), może bez trudu w ciągu prawie dwóch godzin odtworzyć stary rekord Guilloda i Filiatre'a z r.1966 i machnąć sobie ze ćwierć miliona cyfr znaczących. Oczywiście nie za pomocą (skradzionej) Mathematici Wolframa, bo to by trwało całą noc, ale np. zapuszczając program o nazwie Pari - tyleż brzydki, co szybki - a przy tym dostępny za darmo. (Dla zainteresowanych bliższe szczegóły: można go znaleźć w math.ucla.edu albo megrez.math-u-bordeaux.fr. Jest to w zasadzie program dla matematyków-teoretyków, specjalizujących się w teorii liczb. Dla wszystkich jednak może to być znakomity, SZYBKI kalkulator zawierający m. in. liczne funkcje specjalne. Lojalnie ostrzegam: Pari nie jest specjalnie "user friendly".)

Oczywiście, cały ten sport (jak każdy sport) nie służy absolutnie zrozumieniu czegokolwiek. Czy jednak wszystko musi zawsze czemuś służyć?

W tym miejscu musiałem, niestety, przerwać pisanie mojej płomiennej odezwy, bowiem usłyszałem, tak dobrze mi znane, donośne nawoływania i śmiechy. W chwilę później do pracowni wkroczył pan Z. Bardzo z siebie zadowolony powitał mnie wylewnie, przysunął sobie krzesło do mojego, a potem zaczął badawczo wpatrywać się w pisany przeze mnie tekst. Co gorsze, komentował też na głos, z niekłamanym zdumieniem, formuły matematyczne, które zaraz w nim wypatrzył: - A cóż to znowu takiego? Ludzie, ale wzoooryyyy!!! - ekscytował się coraz bardziej.

Z najdalszych nor i zakamarków budynku wybiegli rozmaici, mniej lub bardziej wybitni, uczeni i zgodnym chórem głosów pełnych zgorszenia dołączyli do pana Z. Starałem się za wszelką cenę trzymać fason. Niestety, w tej sytuacji zacząłem z miejsca robić paskudne błędy ortograficzne, na które wszyscy wybrzydzali z niesmakiem. W końcu, z tego wszystkiego, nie wytrzymałem nerwowo: przerwałem pisanie i wydrukowałem szybko to, co mi się udało sklecić. (Pan Z. usiłował wyrwać mi kartki, ale mu zwiałem roztrąciwszy tłum ciekawskich.) Z daleka słyszałem jeszcze, jak komentuje moją ucieczkę: "Ale nerwowy! Czy on tak zawsze? Ciekawe dlaczego?"

W chwilę później ujrzałem, jak maszerują wszyscy zgodnie do kuchni na swój kolejny w tym dniu ciepły posiłek. Idąc parami śpiewali dziarsko (trochę fałszując) osławiony Hymn Postępowych Informatyków:

A oto libretto tego osobliwego "dzieła" - tak, jak go zapamiętałem (pisownia oryginalna; za treść - prymitywną i budzącą raczej mieszane uczucia - nie biorę żadnej odpowiedzialności):

1. Tylko dziwak albo sknera
wciąż zapuszcza Kajrajtera.
Refren: Aby nauka nie szła w las -
Pascal albo Si-Plas-Plas!

2. Jeśli jeszcze nie znasz Łorda
jesteś zakazana morda!

3. Programując we FORTRAN-ie,
możesz dostać tęgie lanie!

4. Dzisiaj nawet każdy klecha
chwali sobie teksty z T_EXa.

5. W każdym razie, do cholery,
niechaj żyją komputery!

W tej sytuacji, na wszelki wypadek zabarykadowałem się w swoim gabinecie, gdzie postanowiłem nieco odpocząć i zebrać wzburzone myśli. Licho wie, co im tam jeszcze może przyjść do głowy! Lepiej uważać. Prawdę mówiąc, ja także, gdy nikt tego nie widział, używałem poczciwego ChiWritera i niemodnego FORTRAN-u, uważając, że ważniejsza jest skuteczność oraz zdrowie psychiczne, niż informatyczne nowinki okupione nerwicą i częstym a kosztownym bebeszeniem komputera.

I właśnie wtedy, gdy tak sobie siedziałem pogrążony w ponurych rozmyślaniach, gdzieś z oddali, doleciał do mnie głos radiowego spikera:

- Tu Polskie Radio Kraków. Zbliża się godzina dwunasta. Obserwatorium Astronomiczne Uniwersytetu Jagiellońskiego (powstałem z szacunkiem). poda czas. piąty, ostatni krótki sygnał oznacza punktualnie. pi, pi, pi, pi, pii, .

Zrobiło mi się słabo.

Dopiero w domu, już na spokojnie, dopisałem następujące:

Zakończenie,

mojej odezwy, czyli tzw. post scriptum (nie mylić z Postscriptem) skierowane do tych nielicznych Uczonych, którym od sterczenia przy komputerach, klikania w ikony, mejlowania i nałogowego buszowania po śmietniskach Internetu nie wyłączyły się jeszcze ich mózgi. Gdyby tak ktoś z Was chciał przypadkiem dostać Medal Fieldsa⁹, a tym samym zapewnić sobie tanim kosztem permanentną pozycję w dowolnej Poważnej Instytucji Naukowej¹⁰, niechaj się zastanowi, czy istnieją może jakieś inne wielomiany a(n) oraz b(n), dla których zachodzi również

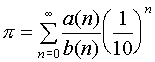
Uczeni! Porzućmy, choć na chwilę, jałowe błąkanie się - niczym pokutujące dusze - po zwodniczych bezdrożach Internetu, wspaniałym stacjom królestwie złego Mejle-Selassie! Dajmy odetchnąć naszym roboczym! W ciszy, zapuśćmy odważnie nasze której nie mąci zwodniczy szum wentylatorów od zasilaczy leżące odłogiem odległych, czasach. I mózgi tak, jak to było w dawnych, choć nie tak w końcu jeszcze znajdźmy wreszcie te nieszczęsne a(n) oraz b(n), dłużej, niż najbardziej które na pewno przetrwają znacznie nawet efektowne symulacje i fitowania!

Odezwa wisiała w kuchni Obserwatorium przez parę dni. Ten i ów rzucał na nią okiem i znacząco stukał się w czoło. Wreszcie zniknęła. Zdarzyło się to akurat tego dnia, gdy w pobliskiej ubikacji zabrakło papieru toaletowego. Miałem wówczas skrytą nadzieję, że to tylko czysty przypadek. Dziś nie jestem już tego taki pewien.

Unhappy end

Opisane wydarzenia miały swój dramatyczny epilog kilka dni później. Właściwie powoli zaczynałem już zapominać o tej historii. Zresztą całe miasto żyło wtedy nieoczekiwanym skandalem w związku z rzekomym dowodem sławnej hipotezy Riemanna¹¹ o nietrywialnych zerach funkcji zeta. (Poszło o to, że jakiś stuknięty amator narobił szumu, jakoby miał ów upragniony dowód, którego profesjonalni matematycy nie mogli znaleźć przez ponad 130 lat. Naiwny.)

Wracałem późną nocą do domu po referacie na ten temat owych sfałszowanych zer, na którym prelegent - dostojny i utytułowany profesor - błyskotliwie zdemaskował żenujące luki w "dowodzie" bezczelnego ignoranta. Było już dobrze po północy, bowiem burzliwa dyskusja ciągnęła się długo, doszło do rękoczynów, mordobicia, zamieszek ulicznych i rabowania sklepów - tak, że w końcu musiała interweniować policja z armatkami wodnymi. Tłum rozwścieczonych matematyków, który już wcześniej zajął lokalną radiostację, skąd szły w eter jakieś abstrakcyjne komunikaty, chciał nawet dokonać okrutnego samosądu na nieszczęsnym, samozwańczym odkrywcy i niechybnie doszłoby do tego, gdyby policjanci nie odstawili go opancerzonym autem do dobrze strzeżonego aresztu.

Rozmyślając o tym wszystkim zupełnie nie zauważyłem, jak drogę zastąpiło mi dwóch zamaskowanych osobników. Zanim zdążyłem zrobić cokolwiek, jeden z nich boleśnie wykręcił mi ręce, a drugi podsunął pod nos jakiś papier. W mdłym świetle ulicznej latarni rozpoznałem swoją niedawną odezwę.

- Poznajesz to, ty. - i tu posypały się rozmaite niewybredne obelgi. - Wzorów ci się zachciało, kanalio, wyśmiewać się z naszej ciężkiej pracy, nosa zadzierać! Będziesz ty jeszcze szorował dane obserwacyjne z ruskiego satelity, już ja się o to postaram, bydlaku!

Zdrętwiałem cały ze strachu, nogi uginały się pode mną. Pod żebrem czułem lufę obrzyna.

- Zapamiętaj sobie: w przyszłości żadnych takich wyczynów! - wycharczał z tyłu ten, który mnie trzymał. Pomimo przerażenia zastanawiałem się bezwiednie: skąd ja znam ten obleśny głos?

- Tym razem to tylko ostrzeżenie - dodał jeszcze. - Ale już definitywnie ostatnie. Następnym razem znajdą cię sztywnego w ciemnym zaułku, z wyprutymi flakami!

Na wpół przytomny ze strachu dowlokłem się jakoś do swego mieszkania. Było splądrowane. Co jednak ciekawe, antyki i precjoza pozostały nietknięte. Niestety, nie można było tego powiedzieć o mojej pięknej kolekcji egzotycznych, wolno zbieżnych szeregów hipergeometrycznych. Zbrodnicze ręce porozbijały je co do jednego i rozwłóczyły po podłodze ich resztki. Ocalał natomiast bezcenny zbiór rzadkich, zbieranych całymi latami okazów osobliwych całek z wyższych funkcji transcendentnych, który, szczęśliwym zbiegiem okoliczności, akurat dzień wcześniej zgodziłem się wypożyczyć na wystawę do British Museum w Londynie. Spoczywały wszystkie, starannie opakowane, w kilku solidnych skrzyniach w piwnicy domu. Doprawdy, strach nawet myśleć, jaki spotkałby je los, gdyby złoczyńcy zapuścili się i tam.

Natomiast jedyną rzeczą, której zupełnie nie mogłem się doszukać w pozostawionym przez nieznanych intruzów bałaganie, było nader cenne, bibliofilskie wydanie sławnych Tablic całek, sum, szeregów i iloczynów Ryżyka i Gradsteina [4], w czerwonej skórze, na papierze czerpanym (prezent ślubny od przyjaciół). Zniknęło bez śladu, a pancerny sejf, w którym je przechowywałem, ział teraz smętnie osmaloną, ciemną czeluścią, rozpruty potężnym ładunkiem wybuchowym.

I jeszcze jedno: na obitej jedwabiem ścianie salonu ujrzałem ze zgrozą, wymalowany czerwoną farbą z rozpylacza (dość nawet fachowo), wielki dysk akrecyjny z dorodną czarną dziurą w środku. Najwyraźniej jako ostrzeżenie.

Literatura

[1] David H. Bailey, Jonathan M. Borwein, Peter B. Borwein and Simon Plouffe: The Quest for Pi (nie opublikowany raport CECM, Simon Frazier University, British Columbia, 25 June 1996)

[2] H. R. P. Fergusson i D. H. Bailey: Analysis of PSLQ, An Integer Relation Algorithm, manuskrypt 1996 (dostępny u autorów na indywidualną prośbę)

[3] Yasumasa Kanada, Historia Pi, Tokyo-Toshyo Co. Ltd., Tokyo, 1991 (po japońsku)

[4] Israil Solomonovich Gradstein, Yosif Moiseyevich Rizhikh, Tablicy integralov, summ, riadov i proizvedeni, Moscow, "Nauka", 1971 (po rosyjsku)

(Wszelkie podobieństwo występujących w tym opowiadaniu postaci do realnych osób jest czysto przypadkowe.)

Przypisy

¹Tradycyjna już prośba do wszystkich postępowych CAMK-owców (w szczególności do P. T. Anonimowego Recenzenta moich Esejów o Kosmologii Współczesnej) o cierpliwą wyrozumiałość w związku z cytowaniem tu dzieła tak wstecznego - z ich punktu widzenia - jak Biblia.

²Chodzi tu o tzw. "morze miedziane" - wielki zbiornik wody na kapłańskim dziedzińcu świątyni Salomona w Jerozolimie.

³Niejaki Chr. ButterMilk, naiwny teoretyk, były kosmolog, podpowiada mi tu inne wyjaśnienie tego faktu. Możliwe, że pod budowę świątyni Salomon wybrał miejsce o wyraźnie dodatniej krzywiźnie przestrzennej i stąd ta rozbieżność. Nie przychylam się do takiej interpretacji, bowiem przypuszczam, że Chr. ButterMilkiem powodują płytkie ambicje zrobienia na takim gadaniu prywatnej kariery.

⁴Pierwsze trzy najsławniejsze stałe Matematyki to: 0 (zero), 1 (jeden) oraz i (pierwiastek z -1). Piątą jest podstawa logarytmów naturalnych e, szóstą stała Eulera-Mascheroniego gamma, a siódmą stała niejakiego Apéry'ego, czyli zeta(3) (zeta Riemanna w punkcie 3), dowód niewymierności której wprawił w osłupienie matematyków zgromadzonych na kongresie w Helsinkach w roku 1978. Pozostałe stałe, w liczbie kilkunastu: Catalana, Landaua (ale nie tego od Lifszyca), Chińczyna, Feigenbauma i in., nie były jak dotąd potrzebne do szczęścia wielmożnym Astronomom, zatem je tu pominę.

⁵"nadzwyczaj" - to bardzo delikatnie powiedziane.

⁶Matematyka ma - w przeciwieństwie do innych gałęzi wiedzy (np. astrofizyki) - tę cenną zaletę, dzięki której o poprawności danego wyniku można przekonać się osobiście, tj. nie czekając na werdykt humorzastych recenzentów.

⁷"niewiarygodnie" - to także bardzo delikatnie powiedziane.

⁸"wściekle" - to, mimo wszystko, wciąż bardzo delikatnie powiedziane.

⁹To taka matematyczna imitacja Nagrody Nobla. Nawiasem mówiąc: robią go ze złota. Natomiast sam Nobel nie ustanowił matematycznej wersji swej sławnej nagrody, bowiem (podobno) jakiś wredny matematyk odbił mu żonę.

¹⁰Jednak za wyjątkiem CAMK-u, który jest znacznie powyżej takich przyziemnych problemów.

¹¹Jest to obecnie najważniejsza z nie dowiedzionych hipotez matematycznych. Niewykluczone, że ostatecznie okaże się fałszywa. Jednak dowód jej ewentualnej prawdziwości pociągnąłby za sobą ważne i daleko idące wnioski w teorii liczb. Hipoteza ta powiada, że wszystkie zespolone zera funkcji zeta(s) leżą na prostej Re s = 1/2. Jeszcze w roku 1914 niejaki G. H. Hardy dowiódł, że na tej prostej leży nieskończenie wiele zer. Wciąż nie wiadomo, czy są tam wszystkie.