Albert Einstein
Od Redakcji - Przedstawiamy pracę Einsteina pod tytułem "Ist die Trägheit eines Körpers von seinem Energieinhalt abhängig?", złożoną do druku Annalen der Physik 27 września 1905 roku. Po raz pierwszy pojawia się w niej słynny wzór E=mc2, jednak w nieco innej postaci - Einstein oznaczył energię przez L, natomiast prędkość światła przez V.
Wyniki opublikowanych wcześniej dociekań doprowadzają nas do bardzo interesującego rezultatu, którego wyprowadzenie podaje ten artykuł.
W poprzednim rozważaniu korzystałem, prócz równań Maxwella-Hertza dla próżni i prawa Maxwella dla elektromagnetycznej energii przestrzeni - także z następującej zasady. Prawa, według których zmieniają się stany układów fizycznych, nie zależą od tego, do którego z dwóch układów współrzędnych poruszających się jednostajnie i prostoliniowo względem siebie - odnoszą się te zmiany stanu (zasada względności).
Wychodząc z tego doszedłem w szczególności do
następującego rezultatu (patrz §8 cytowanej pracy). Niech
układ płaskich fal świetlnych rozpatrywany w układzie
współrzędnych (x,y,z) posiada energię l i niech
kierunek promienia (prostopadła do czoła fali) tworzy kąt 
z osią x układu. Jeżeli
wprowadzić nowy układ współrzędnych (
,
,
) poruszający się
jednostajnie i prostoliniowo względem układu (x,y,z) i jeżeli
początek pierwszego układu porusza się z prędkością v
wzdłuż osi x, to wspomniana energia światła mierzona w
układzie (,,) wyniesie
gdzie V - prędkość światła. W dalszym ciągu wykorzystamy ten wynik.
Niech w układzie (x,y,z) znajduje się spoczywające ciało,
którego energia względem układu (x,y,z) równa jest E0.
Energia tego samego ciała względem układu (,,) poruszającego się
jak wyżej z prędkością v niech wynosi H0.
Niech ciało to wysyła w kierunku tworzącym kąt z osią x płaską falę świetlną o
energii L/2 [mierzonej względem układu (x,y,z)] i
jednocześnie wysyła taką samą ilość światła w przeciwnym
kierunku. W wyniku tego ciało pozostaje w spoczynku względem
układu (x,y,z). Dla tego procesu powinno być spełnione prawo
zachowania energii i to (zgodnie z zasadą względności)
względem obydwu układów współrzędnych. Jeżeli oznaczymy
przez E1 energię ciała po
wypromieniowaniu światła mierzoną względem układu (x,y,z) i
odpowiednio H1 energię względem układu (,,) korzystając z otrzymanego wyżej związku
znajdziemy:
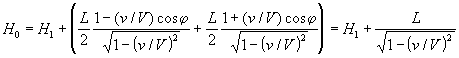
Odejmując drugie równanie od pierwszego otrzymujemy:
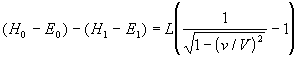
W tym związku obie różnice typu H - E posiadają prosty sens fizyczny. Wielkości H i E reprezentują wartości energii tego samego ciała względem dwóch układów współrzędnych poruszających się względem siebie, przy czym ciało spoczywa w jednym z układów [w układzie (x,y,z)].
W ten sposób jest jasne, że różnica H - E może
odróżniać się od energii kinetycznej K ciała
względem układu [układu (,,)] jedynie o pewną
addytywną stałą C, która zależy od wyboru dowolnych
addytywnych stałych w wyrażeniach dla energii H i E,
zatem możemy napisać H0 - E0
= K0 + C i H1 - E1
= K1 + C, ponieważ stała C przy
emisji światła nie zmienia się. W ten sposób otrzymujemy
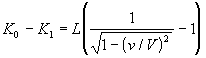
Energia kinetyczna względem układu (,,) zmniejsza się przy
wypromieniowaniu światła o wielkość, która nie zależy od
natury światła. Ponadto różnica K0 - K1
zależy od prędkości dokładnie tak, jak energia kinetyczna
elektronu (patrz §10 cytowanej wyżej pracy).
Pomijając wielkości czwartego i wyższych rzędów można otrzymać
Z tego równania bezpośrednio wynika, że jeżeli ciało oddaje energię L drogą promieniowania to jego masa zmniejsza się o L/v2. Przy czym oczywiście nieistotne jest, że energia stracona przez ciało przechodzi wprost w energię świetlną promieniowania tak, że dochodzimy do bardziej ogólnego wniosku. Masa ciała jest miarą zawartej w nim energii; jeżeli energia zmienia się o wielkość L, to masa zmienia się odpowiednio o wielkość L/9.1020, gdzie energia mierzona jest w ergach a masa w gramach.
Nie wyklucza się możliwości, że teorię uda się sprawdzić dla substancji, których energia zmienia się w dużym stopniu (na przykład dla soli radu). Jeżeli teoria odpowiada faktom, to promieniowanie przenosi bezwładność pomiędzy promieniującymi i pochłaniającymi ciałami.